Understanding Why Motor Phase Current is Different than Power Supply Current

Overview

This paper explains why the current in the windings of a servo drive is different than the DC bus supply current. A power stage H-bridge, connected to a motor winding inductance, is modeled and analyzed during the PWM switching cycle. The balance of motor mechanical power and input electrical power is also discussed.

Understanding the physics

The current that flows through the phases of a motor is lower than the current flowing through the DC bus input because the servo drive behaves as a step-down DC/DC converter. Ignoring the

inefficiencies and commutation details (see Figure 1 below), the product of “input voltage * input current” should be equal to the product of “output current * effective motor voltage”.

In order to understand why the current of the power supply is different than the motor phase current, first, it is necessary to understand how an H-bridge controlling a motor (an inductive load) works. As an example, we are going to use a DC brushed motor with a 2-quadrant switching scheme, as seen in Figure 1:

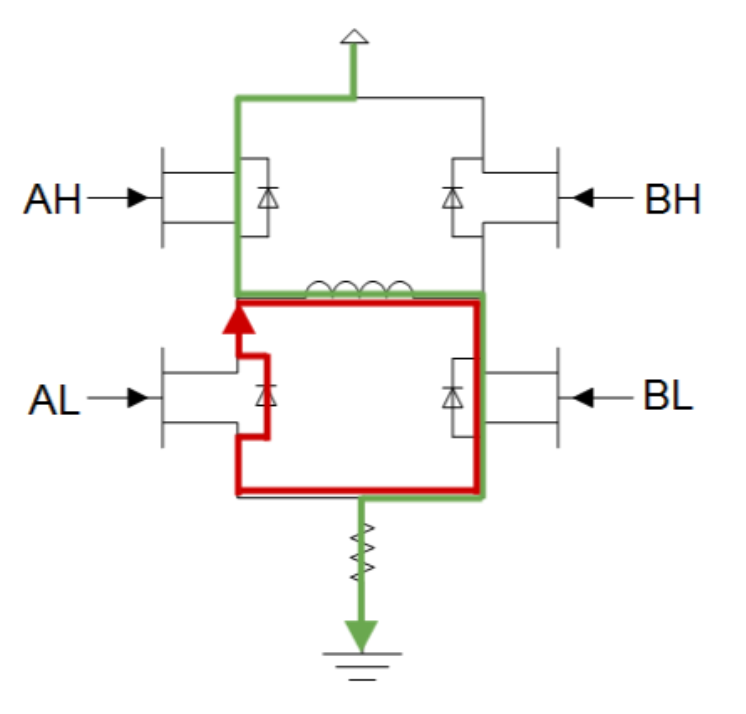
Figure 1

Now we will analyze what happens when switching. The BL transistor is always at 1 state, so it could be modeled as a short circuit. The BH transistor is always at 0 state, so it could be modeled as an open circuit. The AL transistor is always at 0 state but its diode is used for current recirculation so the transistor can be eliminated, and it can be modeled as a single diode. The AH is the switching transistor, therefore its internal diode can be eliminated, and it can be modeled as a single transistor. Finally, taking into account the normal model of a motor, the resulting scheme is shown in Figure 2.

Figure 2

As seen, the model of the motor and its switching grid can be simplified to a DC/DC buck converter. It can be done, with small variations, in a 3-phase grid and with any switching scheme.

Analyzing the model

In order to understand why the current of the motor phases can be greater than the input consumption from the DC bus, it is necessary to apply basic DC/DC converter principles. The current flowing through a buck converter can be divided in two parts during a switching period: the current when the transistor is active (duty), and when the transistor is not active (1-duty). Figure 3 shows the current flowing in both cases.

Figure 3

The current always flows through the motor, but only some of the time  through the DC Bus. Since a motor is inductive, and as the current through an inductor can never change its value instantaneously, when AL transistor switches OFF, the current recirculates through the diode. The current through an inductance is defined by the formula:

The waveform of the voltage and the current during a switching cycle, assuming steady state and continuous conduction mode (which is the normal operation), is shown in Figure 4.

Figure 4

In the T_ON, the inductance is storing energy due to a positive voltage therefore its current rises. In the T_OFF, the current falls due to a negative voltage (equal to – BEMF if we ignore the resistance of the motor) and as a result, the inductance loses energy (transferred to the motor and converted to movement, heating, etc). When measuring the current, the measured value will be the average value of this current ripple.

Now, let’s see why the input current (DC bus) can be different from the output current (motor phases).

As mentioned, the current always flows through the inductor, but only in T_ON  through the AH transistor. This means that the average current  is not equal, and the average value of those currents corresponds to the RMS or DC value. Figure 5 shows it graphically.

Figure 5

Another way to understand this conversion is seeing the switching grid and the inductor as a “black box”, which simply stores energy during T_ON and drops it during T_OFF. Taking that into account, doing a power balance, it can be understood.

Figure 6

In Figure 6, the input voltage, the BEMF, and the output current are fixed values. As Pin=Pout must be equal (inductor cannot store energy forever and a steady state must be reached), the input current value will follow the next formula:

If the voltage of the BEMF is lower than the DC voltage, then the value of the DC current will be lower than the motor current, because the power balance must be maintained. If the motor speed is high, the back electromagnetic force voltage (BEMF) will increase. For a given current, the PWM duty cycle will be higher. This means the motor current can get very close to the power supply current at maximum motor speed (maximum PWM duty cycle).

Conclusion

• The power stage behaves as a step-down switching converter. The effective voltage generated by the driver that goes through the phases of the motor is always equal or lower than the DC bus voltage.
• Therefore, to keep the input and output power balanced, the output current that flows through the motor phases should be higher than the input.
• This gets complicated with PMAC or brushless DC, but the principles are similar to a brushed DC.
• At low speeds the difference between motor and DC bus current is big.
• At high motor SPEED (∝ BEMF), the motor current and power supply will be similar.

This can be understood also from the power balance point of view. Motor mechanical power is speed * torque, while input power is voltage * current.

At low speeds net mechanical power is ~ 0, therefore most of the energy is essentially converted into losses. Only when the speed increases, net power increases.

Figure 7