Motor Constant
The motor constant is the ratio torque to the square root of power and can be utilized in addition to torque and speed to properly size a motor with thermal restrictions in mind. Using the calculated power dissipated and required torque, minimum required motor constant (𝐾𝑚) can be calculated.
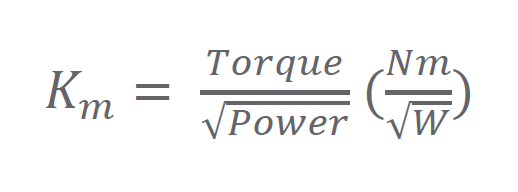 Although it seems this parameter remains constant with the motor, it in fact varies as the temperature of the system fluctuates, because of the changing resistance caused by winding heating. You can see this relationship in the equation below, where 𝐾𝑇 is the torque constant, and 𝑅 is the resistance.
Although it seems this parameter remains constant with the motor, it in fact varies as the temperature of the system fluctuates, because of the changing resistance caused by winding heating. You can see this relationship in the equation below, where 𝐾𝑇 is the torque constant, and 𝑅 is the resistance.
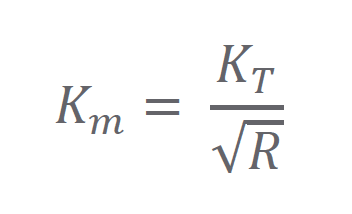
As the resistance increases due to Joule heating, the motor constant decreases. If you have a larger maximum allowable temperature, your motor constant will decrease.
Not all motor manufacturers provide information in the same manner. Some will list 𝐾𝑚 at ambient temperature, rather than a hot temperature, which means that the resistance would be at a minimum. Be aware of this inconsistency and look out for notes on datasheets that state temperatures at which the parameters are calculated.
In the example below, we have two system specifications: torque and speed. Imagine the operating temperature is known but is not communicated at the time of the motor selection process.
| Motor Requirements | |
| Torque | ≥ 0.4Nm of continuous torque |
| Speed | ≥ 900 RPM at maximum continuous torque |
With these specifications in mind, we found a motor. In Figure 1 below, the motor meets the continuous Torque-Speed requirement of 0.4 Nm at 900 RPM.
 Figure 1 – Celera Motion UTH-63-B-24-A-N-000 Motor Torque-Speed Profile at 24Vdc and 90°C temperature rise (130°C Max Temperature)
Figure 1 – Celera Motion UTH-63-B-24-A-N-000 Motor Torque-Speed Profile at 24Vdc and 90°C temperature rise (130°C Max Temperature)
However, when the motor is installed into the housing and operated at the required torque and speed, the temperature exceeds what is allowed for this system at 130°C. If the torque-speed profile was run at the actual maximum operating temperature of 80°C (Figure 2 below), we would have seen the motor’s continuous torque specification fall short.

Figure 2 – Celera Motion UTH-63-B-24-A-N-000 Motor Torque-Speed Profile at 24Vdc and 40°C temperature rise (80°C Max Temperature)
Now, the motor must be replaced, and we must start back at the beginning of the motor selection process.
In the next example, the maximum allowable operating temperature is known, and the required 𝐾𝑚 is calculated in addition to the original torque and speed requirements.
| Motor Requirements | |
| Torque | ≥ 0.4Nm of continuous torque |
| Speed | ≥ 1000 RPM at continuous torque |
| Calculated 𝐾𝑚 | ≥ 0.09 |
If we use the same example shown above, and instead look at the 𝐾𝑚 values on the datasheets, we can verify that the motor in Figure 1 would not meet the system requirements, allowing us to find a new motor that satisfies both temperature limitations and the torque-speed point.
Table 1
Example of Motor Selection with system requirements and two different motors (one is shown at varying max allowable temperatures)
 Note: system required 𝐾𝑚 is calculated.
Note: system required 𝐾𝑚 is calculated.
The example above shows that neglecting the motor constant could be detrimental to the system in terms of safety, MTBF, and accuracy. This also proves how much time could be saved by understanding the required motor constant.



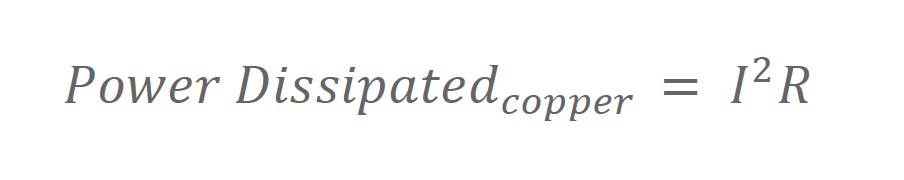 Drive: When the drive delivers current to the motor the power stage heats up due to conduction and switching losses. Celera Motion’s Ingenia Summit Series servo drives are specifically designed to minimize thermal losses and facilitate heat dissipation.
Drive: When the drive delivers current to the motor the power stage heats up due to conduction and switching losses. Celera Motion’s Ingenia Summit Series servo drives are specifically designed to minimize thermal losses and facilitate heat dissipation.

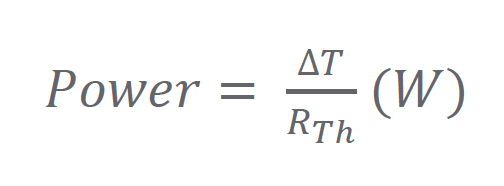
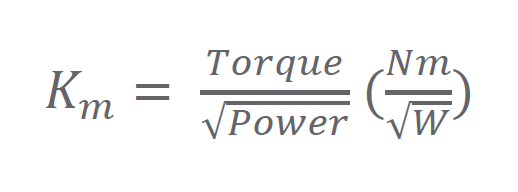 Although it seems this parameter remains constant with the motor, it in fact varies as the temperature of the system fluctuates, because of the changing resistance caused by winding heating. You can see this relationship in the equation below, where 𝐾𝑇 is the torque constant, and 𝑅 is the resistance.
Although it seems this parameter remains constant with the motor, it in fact varies as the temperature of the system fluctuates, because of the changing resistance caused by winding heating. You can see this relationship in the equation below, where 𝐾𝑇 is the torque constant, and 𝑅 is the resistance.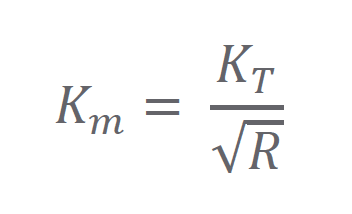
 Figure 1 – Celera Motion UTH-63-B-24-A-N-000 Motor Torque-Speed Profile at 24Vdc and 90°C temperature rise (130°C Max Temperature)
Figure 1 – Celera Motion UTH-63-B-24-A-N-000 Motor Torque-Speed Profile at 24Vdc and 90°C temperature rise (130°C Max Temperature)
 Note: system required 𝐾𝑚 is calculated.
Note: system required 𝐾𝑚 is calculated.



