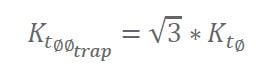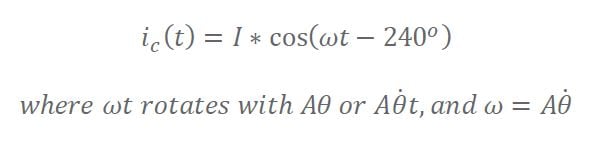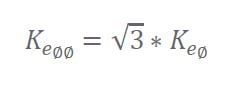Introduction
Calculating motor torque from available drive current can be confusing due to many different drive types and the multiple ways current is specified (Ipk–sine, IDC, IRMS). This paper will provide the key formulas for torque constant and motor current, from fundamental principles of three-phase motor theory. It will also walk through the many ways torque can be calculated, using a per-phase torque, phase-to-phase torque constant, and sinusoidal torque constant, while applying the appropriate currents based on drive type (trapezoidal or sine).
Three Phase Motor Theory
The motor theory described in this paper is based on a brushless motor (BLAC or permanent magnet synchronous machines) configuration that has a sinusoidal back EMF waveform for each phase-toneutral winding. Assumptions are as follows: torque angle curves and current waveforms are assumed to be pure sinusoids of the same amplitude. For equations using the per-phase torque constant, this assumes that input current is supplied to the neutral (center tap) connection.
When applying current to a singular motor phase of a BLAC (phase-to-neutral), these types of motors generate sinusoidal torque waveforms versus electrical angle (as the shaft rotates mechanically). The electrical angle is N/2 multiplied by (*) mechanical angle, where N is the number of poles of the motor.
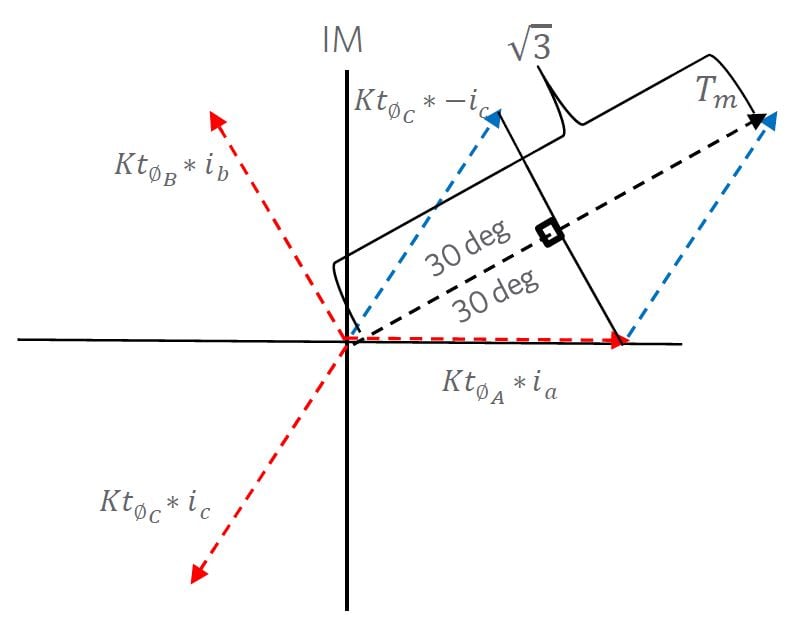
Figure 1 below shows a graphical drawing for the phasor representation of torque angle curve, with a three-phase brushless motor. The three vectors created by 
are shown as dotted lines, meant to represent that these vectors scale up and down in magnitude, as they rotate around the phase diagram, always staying 120 degrees apart. The magnitude of each vector varies based on current 𝑖𝑥 (constant for trapezoidal commutation, and sinusoidal for sine commutation) and the sinusoidal variation of the perphase torque constant (𝐾𝑡∅𝑥) with rotor position.
In this derivation, we are making the assumption that the 𝐾𝑡∅ values are equal in magnitude (actual variations are typically small, but for the purposes of these derivations, we are stating there are no variations), and separated by 120 electrical degrees.
Figure 1 – Spatial Variation of Torque in the Re/Im plane
Trapezoidal Drive
Trapezoidal commutation allows current to only flow through two of the three motor phases at any given time, and the current flowing is considered to be DC (see Figure 2). This results in
𝑖𝑎(𝑡) = −𝑖𝑐(𝑡) & 𝑖𝑎(𝑡) = IDC. For the purposes of the derivation, we are ignoring the ramp up and ramp down of the current based on the time constant (RL) of the motor phases. With this configuration, 𝑖𝑥 values within the phasor diagram of Figure 1 are constant in time and have no variation (unlike sinusoidal drive, which will be discussed below).
Figure 2 – Trapezoidal Current in Three-Phase Motor
The general equation for motor torque is a function of the single-phase motor torque and the current flowing through each of the three phases, represented as follows:
Equation (1)
As stated above for trapezoidal drives, current is only flowing in two of three phases at any one time, so the math reduces significantly, and the motor torque (𝑇𝑚𝑡rap) can be solved algebraically or by using vector math as shown in Figure 3.
Figure 3 – Vector Math for Trapezoidal Commutation
Solving Equation (1) algebraically requires angle 𝐴∅ to be known. From the vector diagram of Figure 3, we can see that when current is only flowing in phase A and out phase C, the value is 30 degrees, and we arrive at Equation (2) below.
Equation (2)
Since current 𝐼𝐷C is only ever flowing in two phases at a time, an equivalent two-phase torque constant is then derived:
Equation (4) yields the result of the two-phase motor torque constant, as a function of the single-phase.
Sinusoidal Drive
Sine drives use a commutation scheme that flows current in all three phases at all times, with the sum always equaling zero (𝐼𝐴+𝐼𝐵+𝐼𝐶 = 0). Different than a trapezoidal drive, the currents 𝑖𝑥 are now modulating sinusoidally as follows:
Where 𝜔t rotates with 𝐴𝜃 or 𝐴𝜃 ̇𝑡 and 𝜔=𝐴𝜃 ̇
Substituting Equations (5), (6), and (7) into Equation (1) yields:
Equation (8)
Solving Equation (8) for where 𝜔t =𝐴∅ and 𝐴∅ = 0° yields:
Like Equation (3) above, which shows torque developed as a function of the single-phase torque constant and the current flowing in the motor, Equation (9) can be re-written to represent a sinusoidal torque constant. Equation (10) yields the equivalent torque constant for current flowing when using a sine drive.
Back EMF Constant and Torque Constant
In Wye connected motors, the center tap (neutral) is rarely available, making phase-to-neutral measurements impossible. The best thing to do is work within the constraints and make phase-to-phase measurements, then work backwards through the equations to arrive at per-phase, phase-to-phase, and sine torque constants.
When working in SI units, the per-phase 𝐾𝑒∅ constant is equal to the single-phase torque constant 𝐾𝑡∅. In a three-phase system, if we could measure a single-phase voltage, we would find that the relationship between single-phase and phase-to-phase voltage is:
This is because 𝐾𝑒 is directly correlated to 𝑉𝑏emf
Given the relationship between 𝐾𝑒 and voltage shown in Equation (12), the voltage output can be substituted for 𝐾𝑒 in Equation (11), yielding Equation (13).
In Equation (4) above, we show how 𝐾𝑡∅∅𝑡rap = √3 ∗ 𝐾𝑡∅ and when combined with 𝐾𝑒∅ = 𝐾𝑡∅ we get:
The two-phase representation 𝐾𝑡∅∅ is then equivalent to 𝐾𝑡∅∅𝑡rap.
Therefore, Equation (13) is also equal to Equation (14).
Comparing Trapezoidal with Sine Commutation
Since measurement of 𝐾e∅∅ (and subsequent conversion to 𝐾𝑡∅∅𝑡rap) involves two phases at a time, it is convenient to find a conversion from 𝐾𝑡∅∅𝑡rap to 𝐾𝑡sine.
We know that 𝐾msine = 𝐾m𝑡rap therefore using Equations (3) and (9), solving for 𝐼𝐷C we see that:
Substituting Equation (15) above into Equation (16), yields Equation (17).
Equation (17)
Simplifying the equation then yields Equation (18).
Equation (18)
It should be noted that referring to 𝐾tsine as a line-to-line or phase-to-phase, torque constant, is generally not good pratice because it implies only two phases are working at once – which is only true for very brief moments when the phase-to-phase current of a single-phase pair passes through zero. It is useful, however, to scale between a two-phase (𝐾𝑡∅∅𝑡rap) and a sinusoidal (𝐾𝑡sine) torque constant, as many drives and motor companies spec current (IDC or Ipk-sine) and torque constant (𝐾𝑡∅∅𝑡rap or 𝐾𝑡sine) differently.
Static Kt Test Versus Ke to Kt Calculation
1. Back drive motor and calculate 
2. Convert 𝐾e∅ to 𝐾tsine and 𝐾t∅∅trap
3. Apply various current outputs (0.1, 0.2, 0.2, and 0.3 𝐴𝑝k-sine) from the drive, using the drive’s software (MotionLab 3)
4. Hold motor shaft in place long enough to get full reading on oscilloscope that is reading torque
5. Record oscilloscope output in volts and convert to oz-in
6. Calculate 4 values of 𝐾𝑡∅ (in units of 𝑁m/𝐴𝑝k-sine) using Equation (10).
7. Use Average to calculate 𝐾tsine .
8. Calculate Percent Error
9. Solve for 𝐾t∅∅trap
10. Calculate Percent Error
Calculations
Calculating 𝐾t∅ for measurements 1 and 2:
1.Current = 0.2 𝐴𝑝k-sine
Tm = 0/94 oz-in = 0.00664
Kt∅ = 0.0221 𝑁m/𝐴𝑝k-sine
2.Current = 0.2 𝐴𝑝k-sine
Tm = 0.92 oz-in = 0.00650
Kt∅ = 0.0217 𝑁m/𝐴𝑝k-sine
Then calculate the average:
Average Kt∅ = 0.0219 Nm/𝐴𝑝k-sine
- Use Average Kt∅ to calculate Ktsine
Ktsine = 1.5 * Kt∅ = 1.5 * 0.0219 𝑁m/𝐴𝑝k-sine = 0.0329 𝑁m/𝐴𝑝k-sine
- Calculate percentage error
Expected Ktsine from datasheet = 0.034 𝑁m/𝐴𝑝k-sine
Expected Ktsine from measured = 0.033 𝑁m/𝐴𝑝k-sine
- Solve for Kt∅∅trap
Average 𝐾t∅ = 0.0219 𝑁m/𝐴𝑝k-sine
𝐾t∅∅𝑡rap = √3 * 0.0219 = 0.038 𝑁m/𝐴DC
Expected Kt∅∅trap from datasheet = 0.039 𝑁m/𝐴DC
Expected Kt∅∅trap from measured = 0.038 𝑁m/𝐴DC
Summary of Test Data
For percent error calculations, the measured 𝐾e∅∅ was used as the ‘expected’ value, instead of the motor spec sheet value, due to variations of 10% allowed for magnet strength differences. The calculated 𝐾𝑡sine with <1% error and the calculated 𝐾𝑡∅∅trap of ~3% error are both within the acceptable range given the error of the measurements. The calculations above, conducted with a slotless motor, also eliminate any cogging torque from altering measured data. Cogging torque can have a huge impact on static torque testing and should always be considered. For this reason, back driving motors and using 𝐾=e∅∅trap to arrive at 𝐾𝑡∅∅trap is the preferred approach. The static testing above is also a common method, but can quickly be made irrelevant when cogging is introduced.
Conclusion
The torque constant Kt is a critical motor parameter that determines the amount of output torque per input current. Because of the three-phase nature of brushless DC/AC/PMSM, and how they are driven, confusion quickly arises as to which Kt value to use when calculating output torque for a given input current. The two most common ways to state Kt are Kt∅∅trap with units of 𝑁m / 𝐴𝐷C ⁄ and 𝐾𝑡sine units of 𝑁m / 𝐴pk-sine . The derivation of both comes from per-phase motor theory and the conversion between them has been shown. Care must be taken to understand how the motor will be driven in terms of the drive type, and how the motor manufacturer is stating Kt. When testing to confirm stated Kt values, be cautious when cogging is present. For this reason, it is recommended to back drive motors to measure 𝐾𝑒 and convert to 𝐾𝑡∅∅𝑡rap and 𝐾𝑡sine as shown in this paper.
Acknowledgments
Per-phase torque derivations described in this paper were made possible through a partnership with Dr. Steve Prina, Co-Founder of Applimotion, now part of Celera Motion a Novanta Company
